[BOJ] 백준 2357번 최솟값과 최댓값

Segment tree :)

# BOJ 2357 최솟값과 최댓값

◎ 세그먼트 트리의 개념

개념 참고 링크 1 : 네이버 블로그

개념 참고 링크 2 : BOJ 블로그

개념 참고 링크 3 : BOJBOOK

세그먼트 트리에 대한 개념과 그에 대한 이해는 이상의 사이트들을 참고하여 진행했습니다

결국 이진 트리로 재구성하여 재귀적인 방법 등으로 구간 합을 구하는 자료구조임을 이해했습니다

일반 배열의 탐색 및 수정

	일반 배열	세그먼트 트리
탐색	O(N)	O(logN)
수정	1	O(logN)

◎ if not segment-tree :

만약 이 문제에서 세그먼트 트리나 그에 준하는 자료구조를 쓰지 않는다면?

컴퓨터의 연산 횟수는 보편적으로 1초당 1억 번의 연산을 기준으로 합니다

참고 링크 1: 네이버 블로그

참고 링크 2: 티스토리 블로그

참고 링크 3: 백준 게시판

다시 말해서 일반 배열(리스트)로 접근하면 문제의 N과 M이 각각 최대 10만 == int(1e5),

이를 곱하면 int(1e10)인 100억 즉, 100초가 걸리기에 시간제한인 2초 안에 불가능합니다

세그먼트 트리의 경우 MlogN 이므로 약 160만 번

C++ 기준으로 약 160ms (0.16초)로 수행 가능하고 느린 파이썬으로도 충분히 가능합니다

import math
print(math.log2(int(1e5)))

# result : 16.609640474436812

log 참고 링크 1 : 티스토리 블로그

log 참고 링크 2 : OurCalc

◎ code 작성 → 시간 초과

import sys
input = sys.stdin.readline

def init(start, end, node, nums, tree):
    if start == end:
        tree[node] = [nums[start], nums[start]]
        return tree[node]

    mid = (start+end)//2
    tree[node][0] = min(init(start, mid, node*2, nums, tree)[0], init(mid+1, end, node*2+1, nums, tree)[0])
    tree[node][1] = max(init(start, mid, node*2, nums, tree)[1], init(mid+1, end, node*2+1, nums, tree)[1])
    return tree[node]

def show(start, end, node, left, right, tree):
    if (right < start) or (end < left): return [int(1e9), 1]
    elif (left <= start) and (end <= right):
        return tree[node]

    mid = (start+end)//2
    return [min(show(start, mid, node*2, left, right, tree)[0], show(mid+1, end, node*2+1, left, right, tree)[0]),
            max(show(start, mid, node*2, left, right, tree)[1], show(mid+1, end, node*2+1, left, right, tree)[1])]

def solve():
    N, M = map(int, input().split())
    nums = [int(input()) for _ in range(N)]
    tree = [[0, 0] for _ in range(4*N)]

    init(0, N-1, 1, nums, tree)
    # print(tree)

    for _ in range(M):
        l, r = map(int, input().split())
        print(*show(0, N-1, 1, l-1, r-1, tree))

solve()

최솟값과 최댓값을 하나의 트리로 구할 수 있게 각 노드를 [0, 0]으로 설정하였습니다

하지만 시간 초과가 났기에 게시판의 모든 Q&A를 살펴보며 개선 가능한 부분을 찾았습니다

이유는 크게 2가지였습니다

1. tree 크기를 더 작게 설정할 수 있다
2. (핵심) 재귀의 수행 횟수가 예상치를 크게 웃돈다

◎ 1 - tree 크기 최적화

위 코드는 tree 크기에 대해 4*N을 적용하고 있습니다
경우에 따라 필요치의 약 2배를 차지할 수 있다는 점을 인지하여 개선하였습니다

tree 크기 참고 : 백준 게시판

def cal_tree_len(N):
    tree_len = 1
    while tree_len < N:
        tree_len *= 2   # [1]
    tree_len *= 2       # [2]
    return tree_len

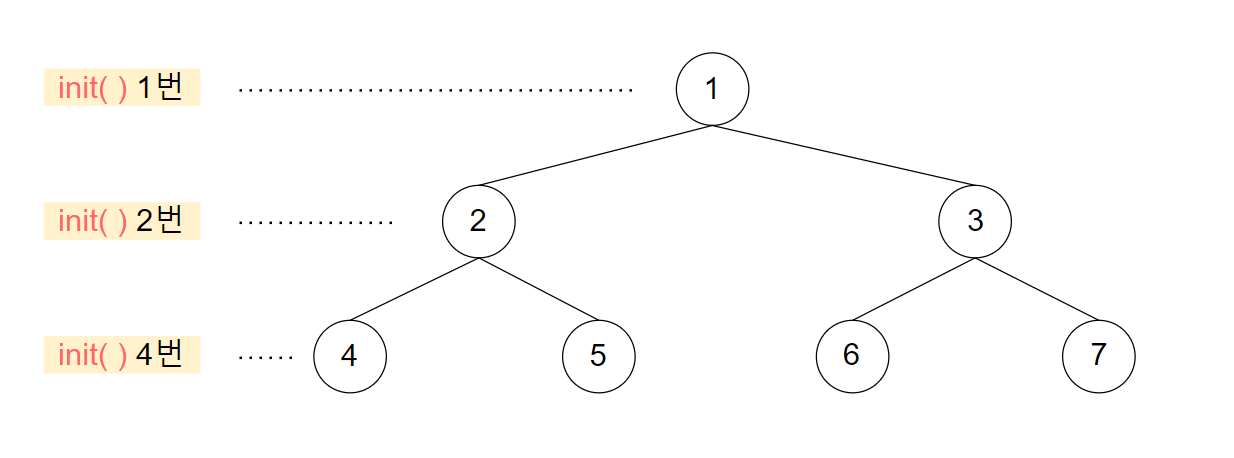
tree의 길이가 2배씩 증가하므로 [ 1 ]까지 수행 했을 때 루트 노드의 level을 1이라 하면
tree_len은 (곱한 횟수 + 1)의 depth를 가지는 포화 이진 트리의 가장 마지막 level의 노드들의 개수와 같습니다

해당 tree_len을 가지는 N의 가능한 가장 큰 N값은 마찬가지로 포화 이진 트리일 때 이므로

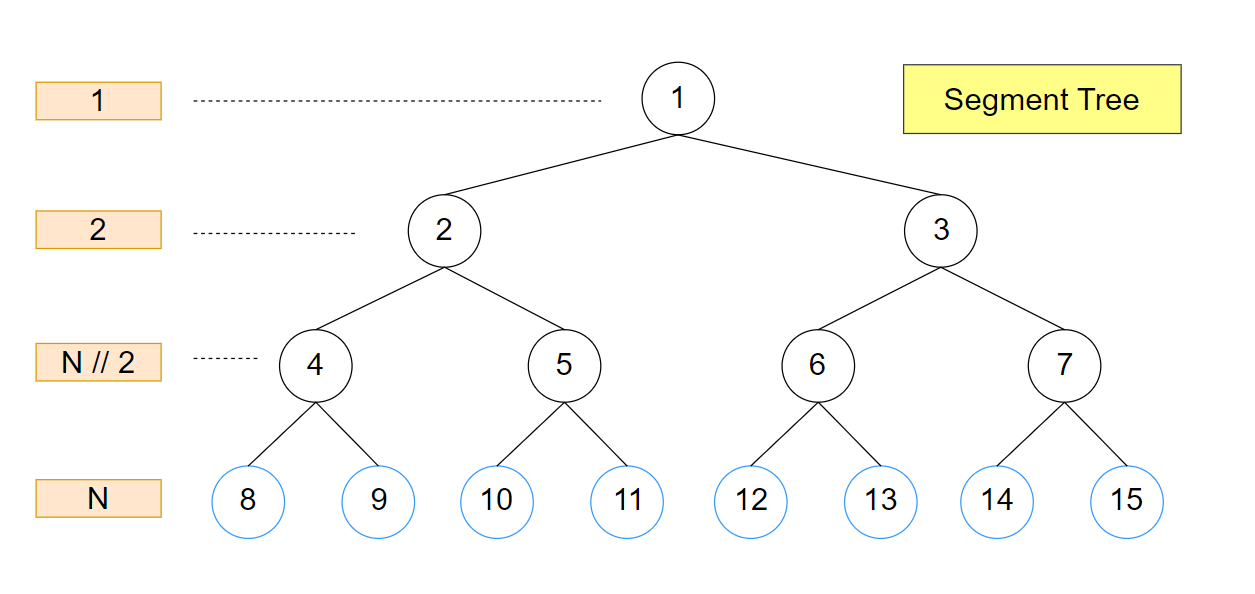
n을 트리의 level, a_n을 해당 level의 노드 수, S_n을 해당 level까지의 총 노드 수라 한다면
a_n은 공비가 2인 공비수열을 이루므로,

여기서 트리의 depth를 d라고 한다면,

따라서 2 * tree_len 은 S_d보다 크므로
[ 2 ]까지 수행했을 때 index error가 발생하지 않는 충분한 크기의 tree로 최적화 할 수 있습니다

◎ 2 - 재귀함수 호출 횟수

게시판을 살펴보니 재귀 함수의 값을 저장해서 반환하는 형식을 취해야 한다는 답변을 보았습니다

재귀함수 호출이나 return 관련 알고리즘에 문제가 있나 싶어 cnt를 찍어보니 예상보다 높습니다

def init(start, end, node, nums, tree):
    global cnt
    cnt += 1

    if start == end:
        tree[node] = [nums[start], nums[start]]
        return tree[node]

    mid = (start+end)//2
    tree[node][0] = min(init(start, mid, node*2, nums, tree)[0], init(mid+1, end, node*2+1, nums, tree)[0])
    tree[node][1] = max(init(start, mid, node*2, nums, tree)[1], init(mid+1, end, node*2+1, nums, tree)[1])
    return tree[node]

def solve():
    N, M = map(int, input().split())
    nums = [int(input()) for _ in range(N)]
    tree = [[0, 0] for _ in range(4*N)]

    global cnt
    cnt = 0

    init(0, N-1, 1, nums, tree)

    print("cnt", cnt)

이유를 살펴보니 init만 봐도 왼쪽 구간, 오른쪽 구간 init()을 2번씩 하기 때문에
2의 배수로 값이 커지는 것이었습니다 input이 이하와 같다면

4 2
1
2
3
4
1 2
2 3

기대 호출 횟수 (cnt) : 13
실제 출력 (cnt) : 21

21 == 1 + (2 * 2) + (4 * 4)

level이 커질수록 2배로 호출하기 때문에 아주 당연하게 시간 초과가 발생합니다
이에 맞춰 코드를 수정하여 통과했습니다 :)

◎ 통과

import sys
input = sys.stdin.readline

def init(start, end, node, nums, tree, check_child):
    if start == end:
        tree[node] = [nums[start], nums[start]]
        return tree[node]

    mid = (start+end)//2
    if check_child:
        tree[node][0] = min(init(start, mid, node*2, nums, tree, True)[0], init(mid+1, end, node*2+1, nums, tree, True)[0])
        tree[node][1] = max(init(start, mid, node*2, nums, tree, False)[1], init(mid+1, end, node*2+1, nums, tree, False)[1])
    return tree[node]

def show(start, end, node, left, right, tree):
    if (right < start) or (end < left): return [int(1e9), 1]
    elif (left <= start) and (end <= right):
        return tree[node]

    mid = (start+end)//2
    left_child, right_child = show(start, mid, node*2, left, right, tree), show(mid+1, end, node*2+1, left, right, tree)
    return [min(left_child[0], right_child[0]), max(left_child[1], right_child[1])]

def cal_tree_len(N):
    tree_len = 1
    while tree_len < N:
        tree_len *= 2
    tree_len *= 2
    return tree_len

def solve():
    N, M = map(int, input().split())
    nums = [int(input()) for _ in range(N)]

    tree = [[0, 0] for _ in range(cal_tree_len(N))]

    init(0, N-1, 1, nums, tree, True)

    for _ in range(M):
        l, r = map(int, input().split())
        print(*show(0, N-1, 1, l-1, r-1, tree))

solve()

BOJ Ruby, Codeforces grandmaster 달성하는 그 날까지 한 걸음씩 : )

• color 참고 : color-hex
• 그림 : draw.io
• Tex (md파일 수식)
  • wiki
  • 수식 error 판단
  • svg 저장
  • md 관련 github